Logistic Regression - Part 1

Mathematical Theory

Sections

Mathematical Model
Model Interpretation
Deriving and Fitting the Model
Comparison with Linear Regression

Mathematical Model

Suppose we want to predict a label \( \hat{y}_i \) based on input features \( \{ x_1, \dots, x_n \} \). Using linear regression, the model that we are fitting to the data is,

\[ \hat{y}_i = \beta_0 + \beta_1 x_1 + \dots + \beta_n x_n. \]

Consider the case when the labels are binary. i.e. \( y_i = 0 \) or \( y_i = 1 \). The linear regression model is unlikely to produce \( \hat{y}_i \) values of exactly \( 0 \) or \( 1 \). In fact, most of the time, values will end up much greater than \( 1 \) or be far below \( 0 \). To get around this problem, we could instead try to fit the logistic regression model,

\[ \hat{p}_i = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + ... + \beta_n x_n)}} = \frac{e^{\beta_0 + \beta_1 x_1 + ... + \beta_n x_n}}{1 + e^{\beta_0 + \beta_1 x_1 + ... + \beta_n x_n}}, \]

Where \( \hat{p}_i \) is the model’s estimate of the probability that \( y_i = 1 \). This estimate is guaranteed to lie between \( 0 \) and \( 1 \). A simple plot of the function \( y = \) on \( z \in [-10, 10] \) demonstrates why this is true.

 1import numpy as np
 2import matplotlib.pyplot as plt
 3
 4z = np.linspace(-10, 10, 100)
 5y = 1 / (1 + np.exp(-z))
 6
 7plt.plot(z, y)
 8plt.xlabel("z")
 9plt.ylabel("y")
10plt.title("Logistic Function")
11plt.grid(True)
12plt.savefig('fig1.png', dpi=300)

Model Interpretation

The two terms following \( \hat{p}_i \) above are simply two different ways of writing the logistic function. A second way of looking at the logistic regression model is that the natural logarithm of the odds \( \frac{ \hat{p}_i }{1 - \hat{p}_i } \) is a linear combination of input \( \{ x_1,...,x_n \} \).

That is,

\[ \ln(\frac{ \hat{p}_i }{ 1 - \hat{p}_i }) = \beta_0 + \beta_1 x_1 + ... + \beta_n x_n. \]

A third and rather intuitive way of interpreting the model is to note that the function \( f(z) = \frac{1}{1 + e^{-z}} \) is greater than \( \frac{1}{2} \) only when \( z > 0 \). If our rule is to assign \( \hat{y}_i = 1 \) only when \( \hat{p}_i > \frac{1}{2} \), then we are looking for a linear separator,

\[ \beta_0 + \beta_1 x_1 + ... + \beta_n x_n > 0. \]

These interpretations highlight the fact that logistic regression is a linear model. There are surprisingly many other ways to interpret the logistic regression model. However, as far as I can tell, there is no precise mathematical reason why this model is the “correct” one in any particular situation.

In fact, the logistic function is very similar to the probit function, which is another popular choice for handling binary classification. Sometimes, the choice of model is arbitrary. "All models are wrong, but some are useful".

Deriving and Fitting the Model

The main motivation for the logit model was the desire to apply linear regression methods to probabilities. The following train of thought might approximate what the creators of the model had in mind and how they arrived at modeling the log odds as a linear combination of input features.

We want the fitted probability \( \hat{p}_i \) to be dependent on input \( \{ x_1,...,x_n \} \) in a way that is somehow linear.
We want \( \hat{p}_i \) to be within the interval \( (0, 1) \).
We want to incorporate diminishing returns, so that it takes a bigger change to make a large \( \hat{p}_i \) larger or a small \( \hat{p}_i \) smaller.

This set of lecture notes contains a discussion about this line of reasoning and goes through the derivation of logistic regression in much greater mathematical detail.

When it comes to fitting the model, the “best” set of parameters \( \{ \beta_0, \beta_1, ..., \beta_n \} \) is defined to be the one that maximizes the probability of generating our data. This is known as maximum likelihood estimation. However, there is no way to solve for these parameters exactly. Numerical methods such as Newton’s method have to be used.

Comparison with Linear Regression

Why don’t we just use linear regression? Well, I gave a couple of reasons in the previous section.

That being said, we could try to use linear regression for binary classification with a two-step process: fit the regression line as usual, pick a threshold, then classify all points with predicted values above this threshold as a \( 1 \). For example, in the figure below, a threshold of \( \hat{y}_i >= 0.50 \) could be used to label \( y_i = 1 \). The Python code for this is a little long have been placed in the article_code.txt file in the attachment section at the top of this article.

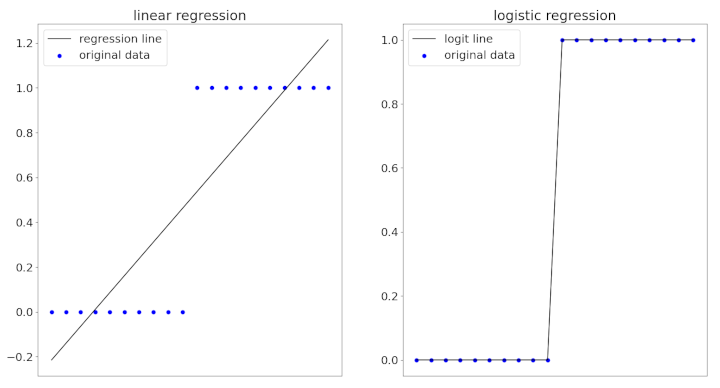
However, since linear regression was not designed for binary classification, this approach can lead to corner cases and anomalies. These figures illustrate yet another possible reason to use logistic regression instead of linear regression: the desire to obtain a closer fit to the data.

With the introduction and mathematical foundations out of the way, we can start working with data in part 2 of this article.