Random Forests Doesn't (Does) Overfit
Overfitting is a machine learning term that is full of rarely discussed nuances and depth. Here, I will attempt to discuss overfitting with regards to random forest models. This article is inspired by the supposedly common saying that “random forest doesn’t overfit”, which was mentioned by the creator himself on his website. We will go through several scenarios demonstrating how random forest does and does not overfit with increasing model complexity. The discussion here will require a good understanding of what the terms “bias” and “variance” mean for machine learning models.
Definition of Overfitting
As far as I know, there isn’t a rigorous mathematical definition of overfitting. It is in fact really difficult to rigorously define overfitting, despite it being extremely intuitive. The wikipedia entry uses this definition taken from the Oxford Dictionary of English:
The production of an analysis which corresponds too closely or exactly to a particular set of data, and may therefore fail to fit additional data or predict future observations reliably.
For the purpose of this article, the inituitive explanation of overfitting that I will be using is this common observation:
The model has much lower training set error than test set error. That is, the model is very well fitted to the training dataset but this performance does not generalize to the test dataset.
Note that just having zero or close to zero error for the training set is not a sign of overfitting. For example, the double descent phenomenon is the observation that large complex machine learning models can achieve zero or close to zero error on training data, while still achieving low errors for test datasets. There is also always the case of perfect separation, which will be illustrated below.
An in-depth mathematical discussion of overfitting can be found in chapter 7 of the very well known and free textbook The Elements of Statistical Learning, second edition.
The Random Forest Model
Leo Breiman’s Random Forest paper is very famous and has a whopping 110,485 citations at the time of writing. The main idea is to use a forest of multiple decision trees and form the output of the model via majority voting.
There are two key elements:
-
Bootstrap aggregating: each decision tree is fitted on a random subset of the data.
-
Random subpsace method: each decision tree is built using a random subset of the feature.
These two elements come together to produce decision trees that are hopefully uncorrelated. A forest of identical trees would be rather pointless!
Binary Classification With Synthetic Data
I will focus on binary classification for this article. Two-dimensional data points are generated from two normal distributions. Data points from one distribution is labeled with a “1” and the other with a “0”. The goal here is to build a random forest model to correctly label new unseen data points as “1” or “0”.
import numpy as np
mean1 = [0, 0]
cov1 = [[1, 0], [0, 1]]
mean2 = [6, 6]
cov2 = [[2, 0], [0, 2]]
gen = np.random.default_rng(seed = 0)
x, y = gen.multivariate_normal(mean1, cov1, 1000).T
a, b = gen.multivariate_normal(mean2, cov2, 1000).T
No Overfitting When Easily Separable
This is an easy case but worth mentioning due to the very common assumption that close to zero training error must mean overfitting. The figure below illustrates extremely separable labels using two normal distributions to generate data points that are relatively far apart.
We can see from the figure that when the data is easily separable, the random forest model is going to have close to zero or zero error on the training set, but the resulting separator will not be overfitted. The yellow and purple decision regions were constructed with the training dataset. All the yellow points (class label = 1) from the test dataset falls nicely in the yellow decision region, while all the purple points (class label = 0) falls within the purple decision region.
Sklearn’s random forest classifier has a score method which I use to show that the training and test set mean accuracy for this case are both equal to 1. Python code to reproduce my results for this section can be found in the easily_separable.txt file in the attachment section at the top of this article.
No Overfitting With More Trees
Next, we examine the infamous phrase “random forest doesn’t overfit”. It is true that random forest doesn’t overfit when the number of trees is increased. This is actually fairly straightforward to explain, following the approach of the textbook The Elements of Statistical Learning, second edition. I am using slightly different notation here. Please refer to Chapter 15.2 on page 589 and Chapter 15.3.4 on page 596 of the 2nd edition if you wish to see the textbook’s version.
Let $ B $ be the number of trees in the model, and $ T_b(x) $ be the output of the $ b $-th tree on input x. Then the random forest model is
Recall that “variance” in machine learning models refers to how close the model is from the average or expected model produced over all possible training sets of the same size. The expected model for the random forest algorithm is in fact
So, we can get arbitrarily close to the expected model by increasing the number of trees $ B. $ This is why variance will decrease as the number of trees are increased.
Overfitting When Increasing Depth
Finally, we look at when random forests can actually overfit. Of course, the data must not be easily separable.
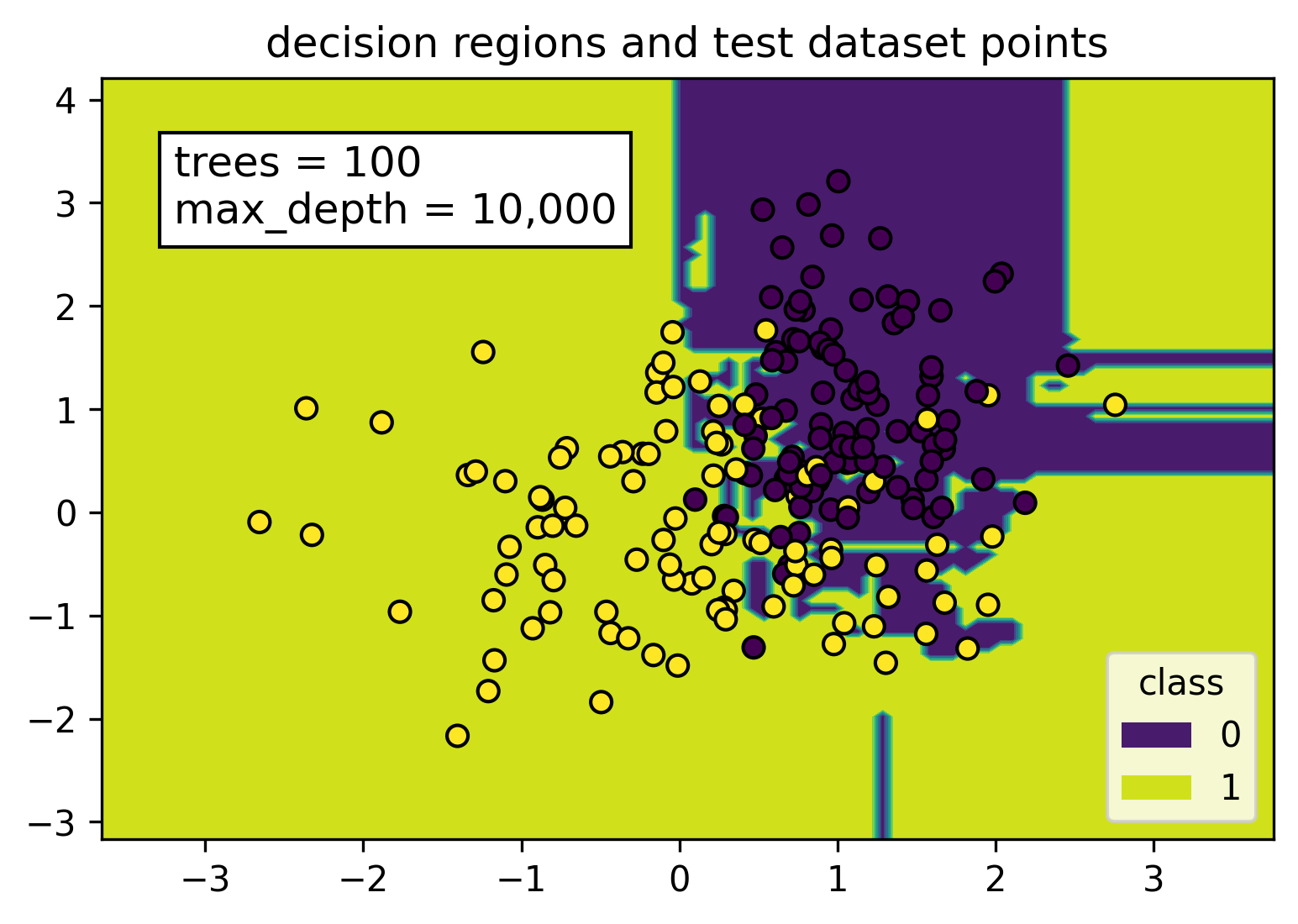
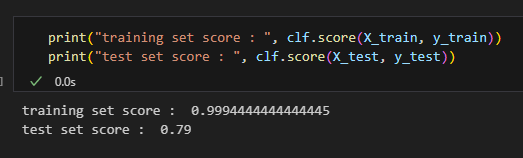
By setting the max depth parameter to 10000, each tree in the random forest model will keep splitting until each node is pure. As seen in the figure, this caused the decision region to be splitted up into tiny irregular chunks. These tiny pieces are tailor made for points in the training set but there is really no reason why they would help classify points from the test dataset.
Hastie’s textbook also talked about this case but still recommends fully grown trees. I am actually not sure what he meant by “fully grown” and the internet offers no help but my guess is that he meant trees that split once on every single one of the randomly selected set of features. This is different from what we have done here, which is to create trees of basically abitrary depth until the nodes are pure.
Resolving the Overfit
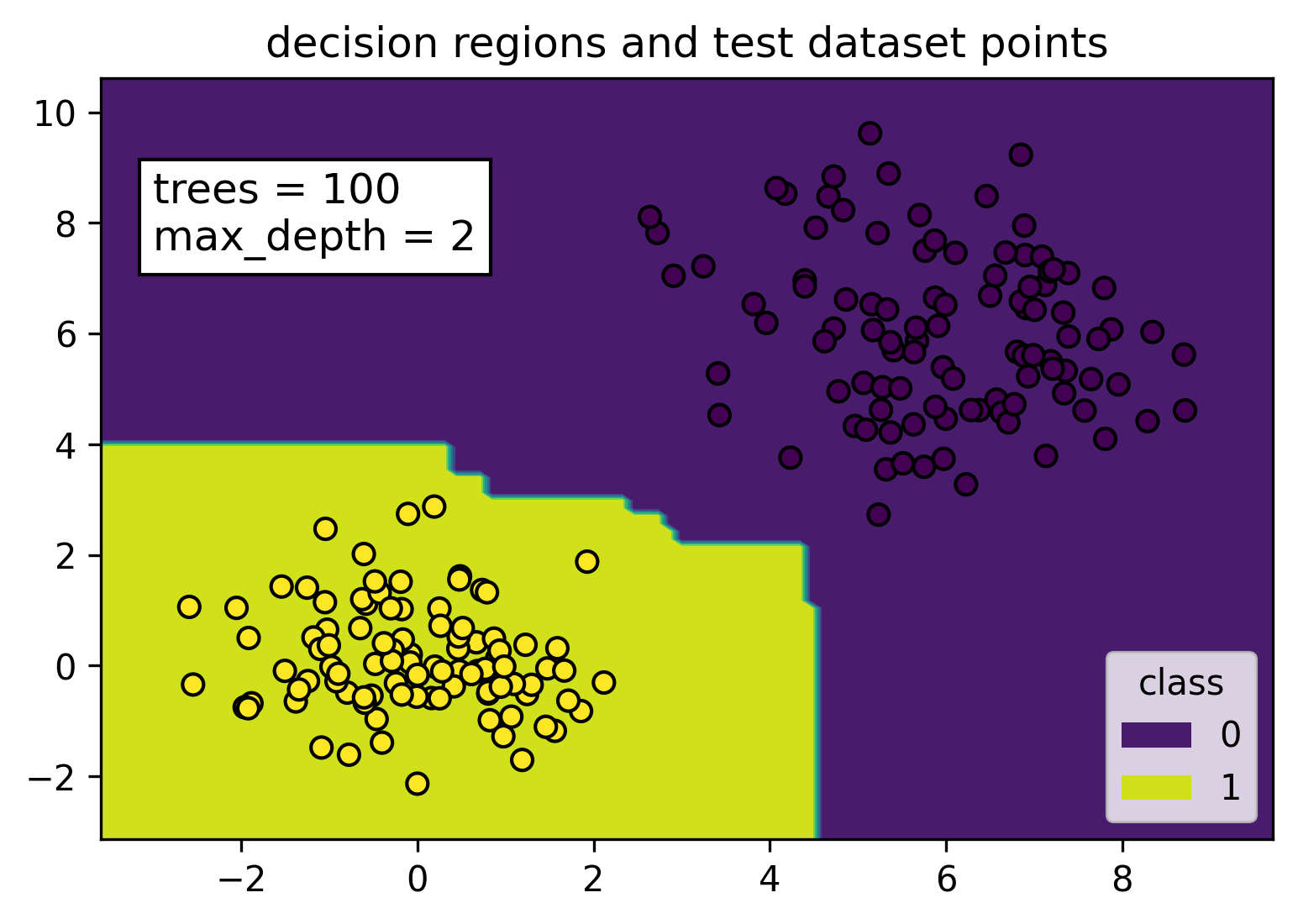
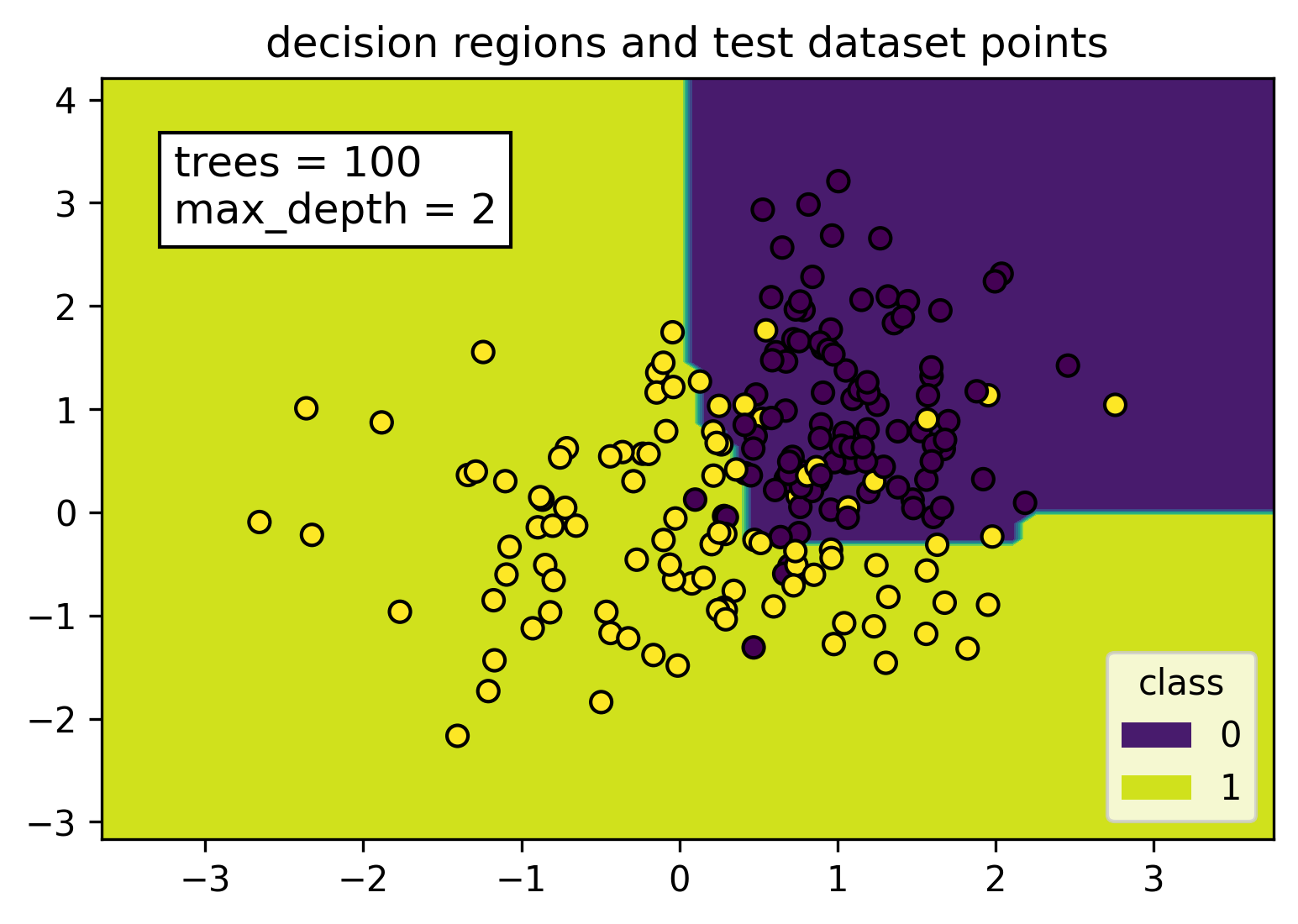
Reducing the max depth parameter to 2 results in a smooth separator dividing the decision region into two, instead of disjoint jagged pieces that we have seen before.
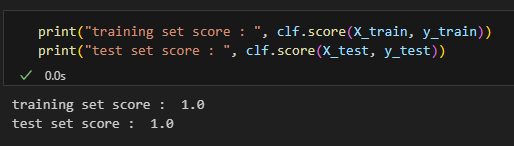
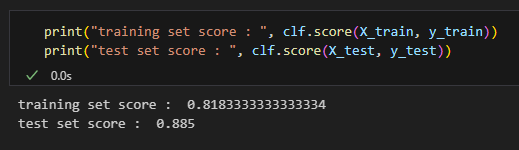
The mean accuracy on the training set decreased but increased for the test set. Like we expected, rededucing the max depth parameter from 10000 to 2 fixed the overfitting problem and made the resulting model more generalizable.
The python code to reproduce this section can be found in the overfit.txt file in the attachment section at the top of this article.